| Предыдущий раздел | Меню навигации | Следующий раздел |
Квадратичная модель (или полиномиальная второго порядка) является простейшей из криволинейных моделей. Она представляется в следующем виде:
![]()
где b0, b1 и b2 - соответственно оценки свободного члена полинома, линейного и квадратичного эффектов. Эти оценки также определяются из условия минимума остаточной суммы квадратов модели Ф, а следовательно их можно найти методом, аналогичным вышеописанному. Желательно правда сместить нуль оси X приблизительно к центру временного ряда для компенсации возможных машинных ошибок округления. В качестве независимых переменных вводятся не только скорректированные значения X, но и их квадраты, зависимой переменной по-прежнему оказывается временной ряд, и в результате расчета мы получаем таблицу, во многом похожую на предыдущую.
Вы можете сразу посмотреть итоговые результаты моделирования уравнением второго порядка объема продаж фирмы Kodak и выводы, либо загрузить таблицу в формате Quattro или в формате Excel и выполнить упражнение, а затем сравнить свои результаты с представленными ниже.
|
Результаты расчета коэффициентов регрессии
| Результат регрессионного анализа | ||
| Константа | 9.021 | |
| Оценка стандартной ошибки Y | 1.035 | |
| Коэффициент вариации | 0.969 | |
| Число наблюдений | 23 | |
| Степени свободы | 20 | |
| Коэффициент(ы) X | 0.800 | 0.022 |
| Стандартная ошибка коэффициента | 0.033 | 0.005 |
| Критерий Стьюдента | 24.599 | 4.064 |
| Табличное значение критерия Стьюдента | 2.086 | |
Наши данные таким образом могут быть описаны уравнением Y = 9.021 + 0.8 * X + 0.022 * X2; именно с использованием этого уравнения был рассчитан прогноз на следующие 4 года (определяемые значениями 12, 13, 14 и 15 после смещения нуля к середине временного ряда). Коэффициент корреляции (обозначаемый в системе Quattro как "коэффициент вариации" - несомненная ошибка перевода программы на русский язык) - несколько возрос по сравнению с линейной моделью, а оценка стандартной ошибки модели несколько снизилась, что говорит об определенных преимуществах регрессии второго порядка по сравнению с линейной в том числе и в отношении ее прогнозных способностей. Рассчитанное межмодельное значение критерия Фишера не слишком велико - 1.739, и это дает преимущества квадратичной модели, но с невысокой доверительной вероятностью, не превышающей 90%.
Наблюдаемые и рассчитанные значения отклика
| Год | Измеренный объем выпуска | Значение X | Значение X2 | Рассчитанное значение |
| 1970 | 2.8 | -11 | 121 | 2.922 |
| 1971 | 3.0 | -10 | 100 | 3.253 |
| 1972 | 3.5 | -9 | 81 | 3.628 |
| 1973 | 4.0 | -8 | 64 | 4.049 |
| 1974 | 4.6 | -7 | 49 | 4.514 |
| 1975 | 5.0 | -6 | 36 | 5.024 |
| 1976 | 5.4 | -5 | 25 | 5.578 |
| 1977 | 6.0 | -4 | 16 | 6.177 |
| 1978 | 7.0 | -3 | 9 | 6.821 |
| 1979 | 8.0 | -2 | 4 | 7.510 |
| 1980 | 9.7 | -1 | 1 | 8.243 |
| 1981 | 10.3 | 0 | 0 | 9.021 |
| 1982 | 10.8 | 1 | 1 | 9.844 |
| 1983 | 10.2 | 2 | 4 | 10.711 |
| 1984 | 10.6 | 3 | 9 | 11.623 |
| 1985 | 10.6 | 4 | 16 | 12.580 |
| 1986 | 11.5 | 5 | 25 | 13.581 |
| 1987 | 13.3 | 6 | 36 | 14.627 |
| 1988 | 17.0 | 7 | 49 | 15.718 |
| 1989 | 18.4 | 8 | 64 | 16.854 |
| 1990 | 18.9 | 9 | 81 | 18.034 |
| 1991 | 19.4 | 10 | 100 | 19.259 |
| 1992 | 20.1 | 11 | 121 | 20.528 |
| Прогнозные значения | ||||
| 1993 | — | 12 | 144 | 21.843 |
| 1994 | — | 13 | 169 | 23.201 |
| 1995 | — | 14 | 196 | 24.605 |
| 1996 | — | 15 | 225 | 26.053 |
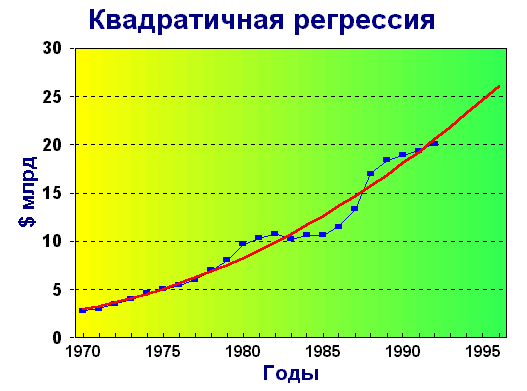
И тем не менее от квадратичной модели следует ожидать лучших прогнозов. В частности если линейная модель предсказывала чистые продажи для фирмы Kodak на 1993 год в объеме 19.6 миллиарда долларов, а это несколько ниже достигнутого уровня для 1992 года, последнего в серии, то квадратичная модель прогнозирует объем 21.84 миллиарда на тот же 1993 год (и как впоследствии оказалось, реальная цифра была близка к этой, и уж во всяком случае укладывалась в интервальную оценку прогноза). Ниже приведено графическое представление рассчитанных прогнозных величин; оно может оказаться полезным для интерпретации результатов.
| Предыдущий раздел | Меню навигации | Следующий раздел |